Occasionally you may want to create an angle that’s congruent to an existing angle. You can also use these methods to help make a triangle or other polygon that’s congruent to an existing triangle or polygon, but can be positioned and rotated as you please while always remaining congruent to the original.
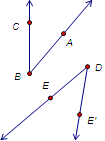
For this construction you’ll use the Transform | Rotate command to make a new angle congruent to an original angle ![]() ABC.
ABC.
1.Use the Ray tool to construct a starting ray DE. This will be the initial side of the new angle. (If you have an existing straight object, you can use it instead of the ray.)
2.Mark endpoint D of the ray or other straight object as the center of rotation by double-clicking it with the Arrow tool. This point will be the vertex of the new angle.
3.Select points A, B, and C that define the original angle, and choose Transform | Mark Angle.
4.Select point E, the other point that determines the initial side of the angle.
5.Choose Transform | Rotate to rotate point E by the marked angle. The rotated image is point E'.
6.Use the Ray tool to construct the ray from D through the new point E'.
7.Test your construction by changing the original angle, and by dragging points D and E that determine the initial side of the new angle.
If you like, use an existing straight object in place of ray DE. You could even use a segment that you've constructed to be congruent to another segment.
To use ASA (Angle - Side - Angle) to construct a new triangle congruent to an existing triangle, begin with a congruent segment. You’ll use this as the initial side of the angles at the two endpoints of the segment. Then use the congruent angle construction twice (steps 2 through 6) to construct two angles, one on each end of the segment, that are congruent to the corresponding angles in the original triangle.
Similarly, you can use SAS to construct a new triangle congruent to an existing triangle. In this case, begin with the congruent angle construction to make an angle congruent to an angle from the original triangle. Then use Construct | Circle by Center+Point to make two circles centered at the vertex of the new angle and with radii equal to the lengths of the two sides of the original triangle. The points where the rays intersect the circles are the other two vertices of the new triangle.
How would you use SSS for the same purpose?
And what happens if you try using SSA?
See also:
How to Construct a Segment of Fixed Length